関数

関数とは

Rは関数型プログラミング言語であり，基本的にほとんどの処理を関数を用いて行う。

関数というのは，なにかを入力すれば，それに応じた出力が得られるものである。入力する「なにか」のことを引数という。関数はfunction_name(引数1, 引数2, ･･･)のような形で用いられる。

たとえば，abs()という関数は，引数として与えられたベクトルの各要素の絶対値を返す。例として，スカラー (長さが1のベクトル)-1を引数として与えてみよう。

abs(- 1)

[1] 1

また，mean()という関数は，引数として与えられたベクトルの要素の平均値を返す。

v <- c(1, 2, 3, 4, 5)
mean(v)

[1] 3

関数の使い方の詳細は，ヘルプを読めばわかる。たとえば，mean()関数の説明を読みたい場合には，?meanと入力すれば良い。

?mean

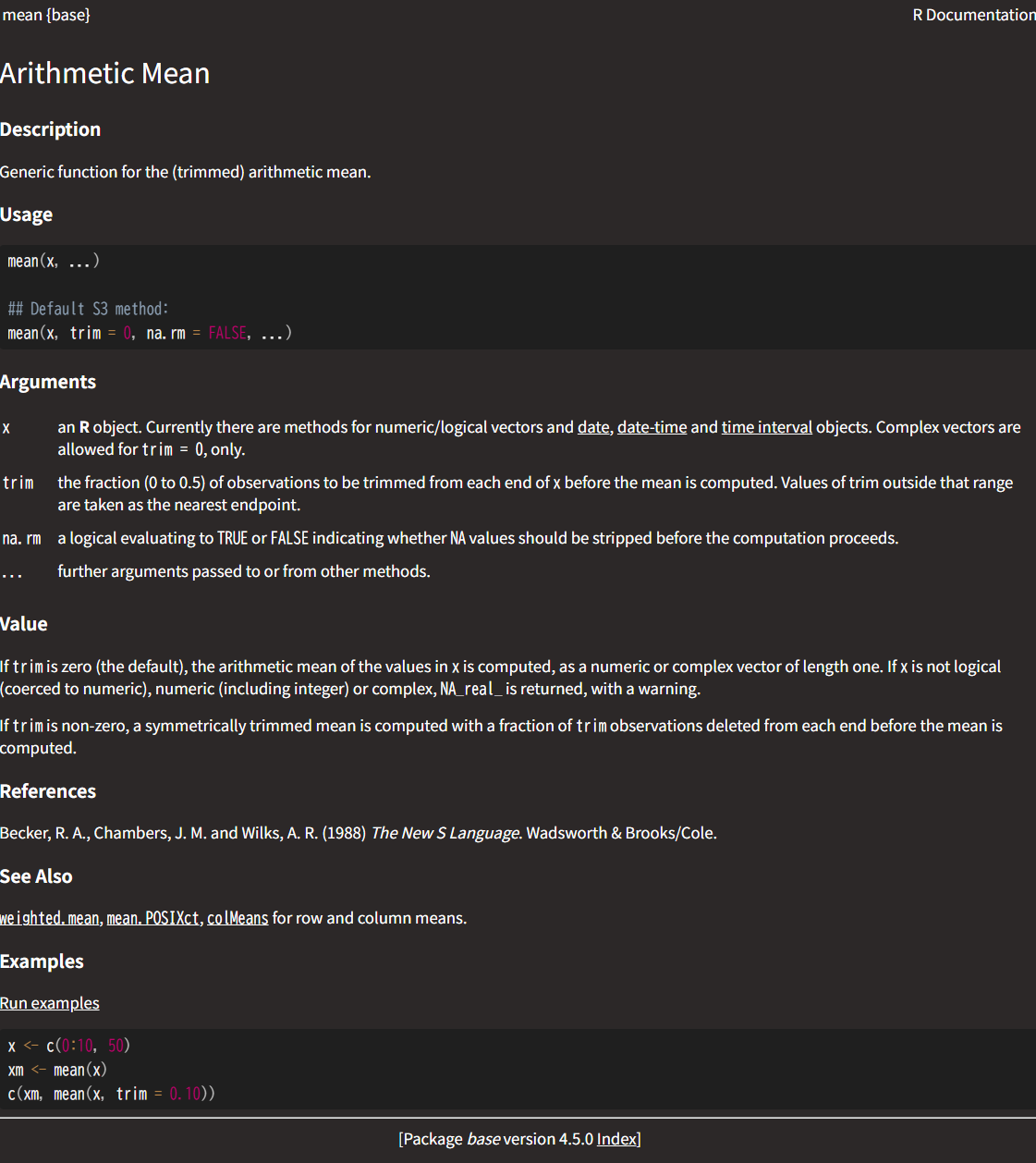
mean()関数の使い方として，以下のように記述されている。

mean(x, trim = 0, na.rm = FALSE, ...)

引数xは平均を計算したいベクトルであるが，それ以外にも引数があることがわかる。これらの引数にはtrimとna.rmという名前がついていて，デフォルトの値 (trimは0, na.rmはFALSE)が設定されている。デフォルトの値が設定されている場合，引数は省略可能である。引数を指定したい場合には，引数名 = 値の形で指定する。

mean()関数は，デフォルトではベクトルにNA (not available，欠損値)が含まれている場合にはNAを返す。NAを除外して平均を計算する場合は，na.rm = TRUEを指定する。

x <- c(1, 2, 3, NA, 5)
mean(x)

[1] NA

mean(x, na.rm = TRUE)

[1] 2.75

関数は，必ずしも何かを計算するためだけに用いるわけではなく，画面に何かを表示させたり，ファイルからデータを読み込んだりといったことにも用いられる。たとえば，q()と入力すればRを終了させることができるが，q()も関数である。

パッケージと関数

Rの関数名は，パッケージ間で競合する場合がある。関数を使う際に，特定のパッケージ (名前空間)に含まれる関数であることを明示的に指定するには，パッケージ名::関数名()のように書く。R本体に組み込まれている関数は，base::関数名()である。また，関数名が競合しない場合でも，パッケージ名::関数名()のように書いておけば，実行するために必要なパッケージが明らかになるという利点もあるので，コードの解説などではこのように記述している場合も多い。ここでは，とくに誤解を生じさせると考えられる場合を除いて，パッケージ名は省略する。

関数の自作

自分で関数を定義することもできる。同じような計算や処理を何度も行うときには，一連の処理を関数として定義しておけば便利だ。

たとえば，順列・組合せを求めたいとしよう。Rには組合せを求める関数としてchoose(n, r)という関数が用意されており，n個のなかからr個を選ぶ組合せが何通りあるかを返す。

たとえば，37個の数字のなかから7個を選ぶ組合せは，以下のように求めることができる。

choose(37, 7)

[1] 10295472

ロト7宝くじというのは，37個の数字のなかから自分が好きな数字を7個選び，それが7つの当選番号とすべて一致すれば一等というクジだ。37個の数字のなかから7個を選ぶ組合せは，ここで計算したように1千万通り以上だから，ロト7で一等が当たる確率は1千万分の1以下ということになる。

次に順列を求めてみよう。Rにはn個の中からr個を取り出す順列を求める関数は用意されていない。そこで，nとrを引数として与えれば，順列を返す関数を自作してみよう。自作の関数は，

関数名 <- function(引数1, 引数2, 引数3 = 0, ...){
  ...処理内容...
  }

の形で定義する。デフォルトの値を設定する場合には，引数名 = 値の形で指定する。この場合，引数3は省略可能で，省略した場合にはデフォルトの値である0が代入される。

n個の中からr個を取り出す順列${}_nP_r$は，

\[{}_nP_r = \frac{n!}{(n-r)!}\]

で計算できる。ただし，$n!=n \times (n-1) \times (n-2) \times \cdots \times 1$であり，これを$n$の階乗という。階乗は，factorial()関数で求めることができる。

順列の計算を行う関数をpermut()として定義しよう。

permut <- function(n, r){
  p <- factorial(n) / factorial(n - r)
  return(p)
}

このコードを実行したら，environmentタブを見てみよう。permutという関数が作成されて表示されているはずだ。

自作の関数permut()の引数はnとrの2つであり，これらを使って${}_nP_r$を計算し，pに代入する。次に，return(p)で順列の計算結果を返す。

return()は関数が返す値を指定するが，これを指定しなければ，関数は最後に行われた計算結果を返す。したがって，permut()関数は以下のように書いても良い。

permut <- function(n, r) {factorial(n) / factorial(n - r)}

ここでは計算が1つしか行われていないので，その結果が返される。

作成した関数を用いて実際に順列を求めてみよう。

permut(10, 4)

[1] 5040

permut(4, 2)

[1] 12

permut(8, 0)

[1] 1

--- title: "関数" --- ## 関数とは Rは関数型プログラミング言語であり，基本的にほとんどの処理を関数を用いて行う。関数というのは，なにかを入力すれば，それに応じた出力が得られるものである。入力する「なにか」のことを引数という。関数は`function_name(引数1, 引数2, ･･･)`のような形で用いられる。たとえば，`abs()`という関数は，引数として与えられたベクトルの各要素の絶対値を返す。例として，スカラー (長さが1のベクトル)`-1`を引数として与えてみよう。 ```{r} abs(- 1) ``` また，`mean()`という関数は，引数として与えられたベクトルの要素の平均値を返す。 ```{r} v <- c(1, 2, 3, 4, 5) mean(v) ``` 関数の使い方の詳細は，ヘルプを読めばわかる。たとえば，`mean()`関数の説明を読みたい場合には，`?mean`と入力すれば良い。 ```{r} ?mean ``` ![ヘルプ](images/R/R_help_mean.png) `mean()`関数の使い方として，以下のように記述されている。 ```{r} #| eval: false mean(x, trim = 0, na.rm = FALSE, ...) ``` 引数`x`は平均を計算したいベクトルであるが，それ以外にも引数があることがわかる。これらの引数には`trim`と`na.rm`という名前がついていて，デフォルトの値 (`trim`は`0`, `na.rm`は`FALSE`)が設定されている。デフォルトの値が設定されている場合，引数は省略可能である。引数を指定したい場合には，`引数名 = 値`の形で指定する。 `mean()`関数は，デフォルトではベクトルに`NA` (not available，欠損値)が含まれている場合には`NA`を返す。`NA`を除外して平均を計算する場合は，`na.rm = TRUE`を指定する。 ```{r} x <- c(1, 2, 3, NA, 5) mean(x) mean(x, na.rm = TRUE) ``` 関数は，必ずしも何かを計算するためだけに用いるわけではなく，画面に何かを表示させたり，ファイルからデータを読み込んだりといったことにも用いられる。たとえば，`q()`と入力すればRを終了させることができるが，`q()`も関数である。 ## パッケージと関数 Rの関数名は，パッケージ間で競合する場合がある。関数を使う際に，特定のパッケージ (名前空間)に含まれる関数であることを明示的に指定するには，`パッケージ名::関数名()`のように書く。R本体に組み込まれている関数は，`base::関数名()`である。また，関数名が競合しない場合でも，`パッケージ名::関数名()`のように書いておけば，実行するために必要なパッケージが明らかになるという利点もあるので，コードの解説などではこのように記述している場合も多い。ここでは，とくに誤解を生じさせると考えられる場合を除いて，パッケージ名は省略する。 ## 関数の自作自分で関数を定義することもできる。同じような計算や処理を何度も行うときには，一連の処理を関数として定義しておけば便利だ。たとえば，順列・組合せを求めたいとしよう。Rには組合せを求める関数として`choose(n, r)`という関数が用意されており，`n`個のなかから`r`個を選ぶ組合せが何通りあるかを返す。たとえば，37個の数字のなかから7個を選ぶ組合せは，以下のように求めることができる。 ```{r} choose(37, 7) ``` ロト7宝くじというのは，37個の数字のなかから自分が好きな数字を7個選び，それが7つの当選番号とすべて一致すれば一等というクジだ。37個の数字のなかから7個を選ぶ組合せは，ここで計算したように1千万通り以上だから，ロト7で一等が当たる確率は1千万分の1以下ということになる。次に順列を求めてみよう。Rには`n`個の中から`r`個を取り出す順列を求める関数は用意されていない。そこで，`n`と`r`を引数として与えれば，順列を返す関数を自作してみよう。自作の関数は， ```{r} 関数名 <- function(引数1, 引数2, 引数3 = 0, ...){ ...処理内容... } ``` の形で定義する。デフォルトの値を設定する場合には，`引数名 = 値`の形で指定する。この場合，引数3は省略可能で，省略した場合にはデフォルトの値である`0`が代入される。 `n`個の中から`r`個を取り出す順列${}_nP_r$は， $${}_nP_r = \frac{n!}{(n-r)!}$$ で計算できる。ただし，$n!=n \times (n-1) \times (n-2) \times \cdots \times 1$であり，これを$n$の階乗という。階乗は，`factorial()`関数で求めることができる。順列の計算を行う関数を`permut()`として定義しよう。 ```{r} permut <- function(n, r){ p <- factorial(n) / factorial(n - r) return(p) } ``` ![自作の関数](images/R/function.png) このコードを実行したら，environmentタブを見てみよう。`permut`という関数が作成されて表示されているはずだ。自作の関数`permut()`の引数は`n`と`r`の2つであり，これらを使って${}_nP_r$を計算し，`p`に代入する。次に，`return(p)`で順列の計算結果を返す。 `return()`は関数が返す値を指定するが，これを指定しなければ，関数は最後に行われた計算結果を返す。したがって，`permut()`関数は以下のように書いても良い。 ```{r} permut <- function(n, r) {factorial(n) / factorial(n - r)} ``` ここでは計算が1つしか行われていないので，その結果が返される。作成した関数を用いて実際に順列を求めてみよう。 ```{r} permut(10, 4) permut(4, 2) permut(8, 0) ```